Day 18
Confidence Interval for a Single Mean
EPSY 5261 : Introductory Statistical Methods
Learning Goals
At the end of this lesson, you should be able to …
- Identify when to answer a research question with a confidence interval.
- Explain the need for creating a confidence interval to do statistical inference.
- Know how to calculate a confidence interval by hand and using R Studio.
- Interpret a confidence interval.
- Explain how the confidence level we choose affects our interval.
Inferential Methods
- Hypothesis Testing
- Answers a yes/no type question
- Example: Is the average movie length longer than 110 minutes?
- Confidence Intervals
- Provides us an estimate taking into account uncertainty
- Example: How long is the average movie?
Confidence Intervals
- We have uncertainty in our sample estimates because of sampling variability (i.e., samples vary)
- We need something to quantify the uncertainty in our estimates.
…
→ Confidence Intervals
Methodology for a Confidence Interval
\[ 95\%~\text{CI} = \text{Sample Statistic} \pm \underbrace{(2 \times SE)}_{\text{Margin of Error}} \] - To get a confidence interval, we add and subtract a specified number of standard errors from the sample statistic.
Determining the SE Multiplier
- Adding and subtracting 2 standard errors gives an estimate for the margin of error.
- In practice, we determine the exact multiplier used in the margin of error by using the t-distribution (for CI for means)
Use t-Distribution
Assumptions
- Data comes from a population with a normal distribution.
- We can proceed if the distribution of the sample looks reasonably normal…OR…
- If the sample size is large enough (\(>30\); CLT)
- In practice, better to use a simulation method to get the standard error (then we don’t need to worry about sample size)
- Independence: must have independent observations
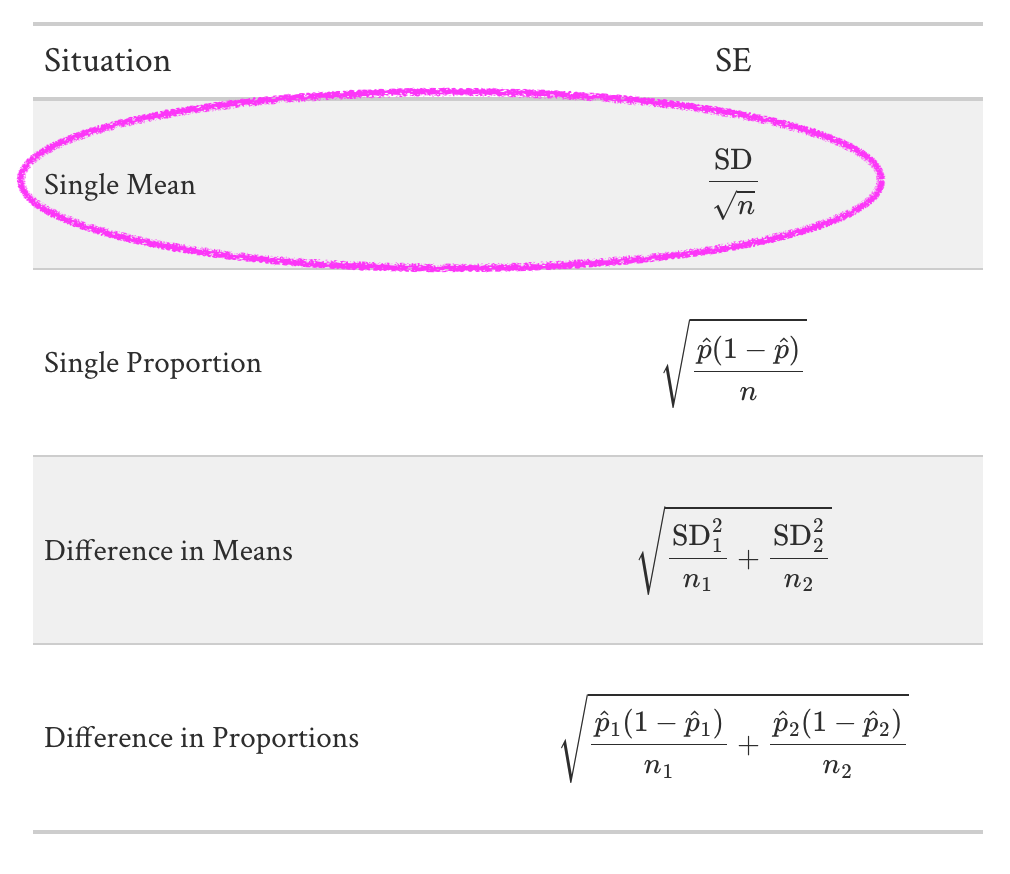
Formula
\[ \text{CI} = \bar{x} \pm (t^* \times \text{SE}) \]
Table 19.1 in Textbook
Formula (Update)
\[ \text{CI} = \bar{x} \pm (t^* \times \frac{\text{SD}}{\sqrt{n}}) \]
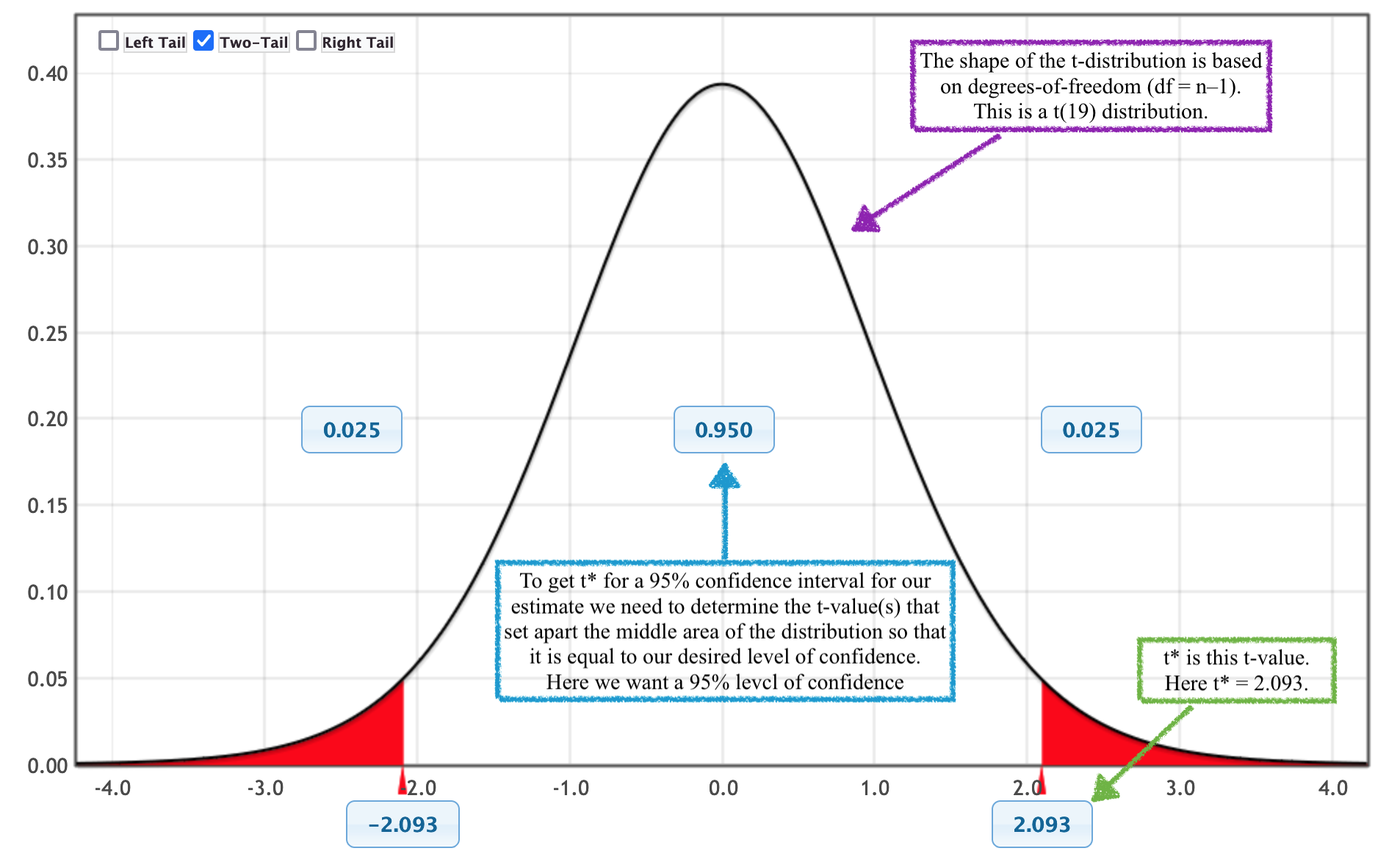
What is \(t^*\)?
- Recall the t-distribution (same one as used for t-test).
- We need to know our degrees of freedom (df)
- We will use this to find the \(t^*\) value based on the desired confidence level.
Example: \(t^*\) for a 95% Confidence Interval
Confidence Interval for a Single Mean Activity
Summary
- For a research question asking for an estimate, the best way to answer is with a confidence interval.
- The confidence interval allows us to account for uncertainty by including sampling variability in our estimate of the parameter.
- With a higher confidence level we expect a larger confidence interval (more uncertainty in the estimate).