Generalization and Random Sampling

The goal in many studies is to provide information about some characteristic of a population. For example, you may want to say something about the percentage of Americans who would support a particular piece of legislation. Or, you may want to provide information about the average amount of time University of Minnesota students take to graduate. One potential solution to obtain such information would be to collect the necessary data from every member of the target population.

In many studies, however, it may not be feasible given time and money constraints to collect data from each member of the population. In these cases it is only possible to consider data collected for a smaller subset, or sample from that population. In these cases, the characteristic of the population would be estimated from the sample data and inferences would be drawn about the population. The key is then to carefully select the sample so that the results estimated from the sample are representative of the characteristic in the larger population. Drawing conclusions about the larger population based on information from a sample is called statistical inference.

VOCABULARY

The population is the entire collection of who or what (e.g., the observational units) that you would like to draw inferences about. A sample is a subset of observational units from the population.

In statistical inference, generalization refers to the approipriateness of using sample data to draw conclusions about the larger population from which the sample was drawn. In practice, statisticians compute a summary measure from their sample (called a statistic) and use it as as estimate for that same summary measure in the population (called a parameter).

VOCABULARY

Population summary measures are called parameters. Sample estimates of parameters are referred to as statistics.

Whether that sample statistic is a statistically good estimate of the population parameter depends on whether the sample is statistically “representative” of the population. In order for the sample to be statistically representative of the population, the sampling units (i.e., cases) in the sample need to have been chosen using an unbiased sampling method—that is, the selection of sample cases has not introduced statistical bias. Statistical bias is when sample statistics differ systematically from the population parameter. The key here is the word “systematically”. This implies that there is something in the underlying process (aside from random variation) that is affecting the estimation process.


Statistical Bias

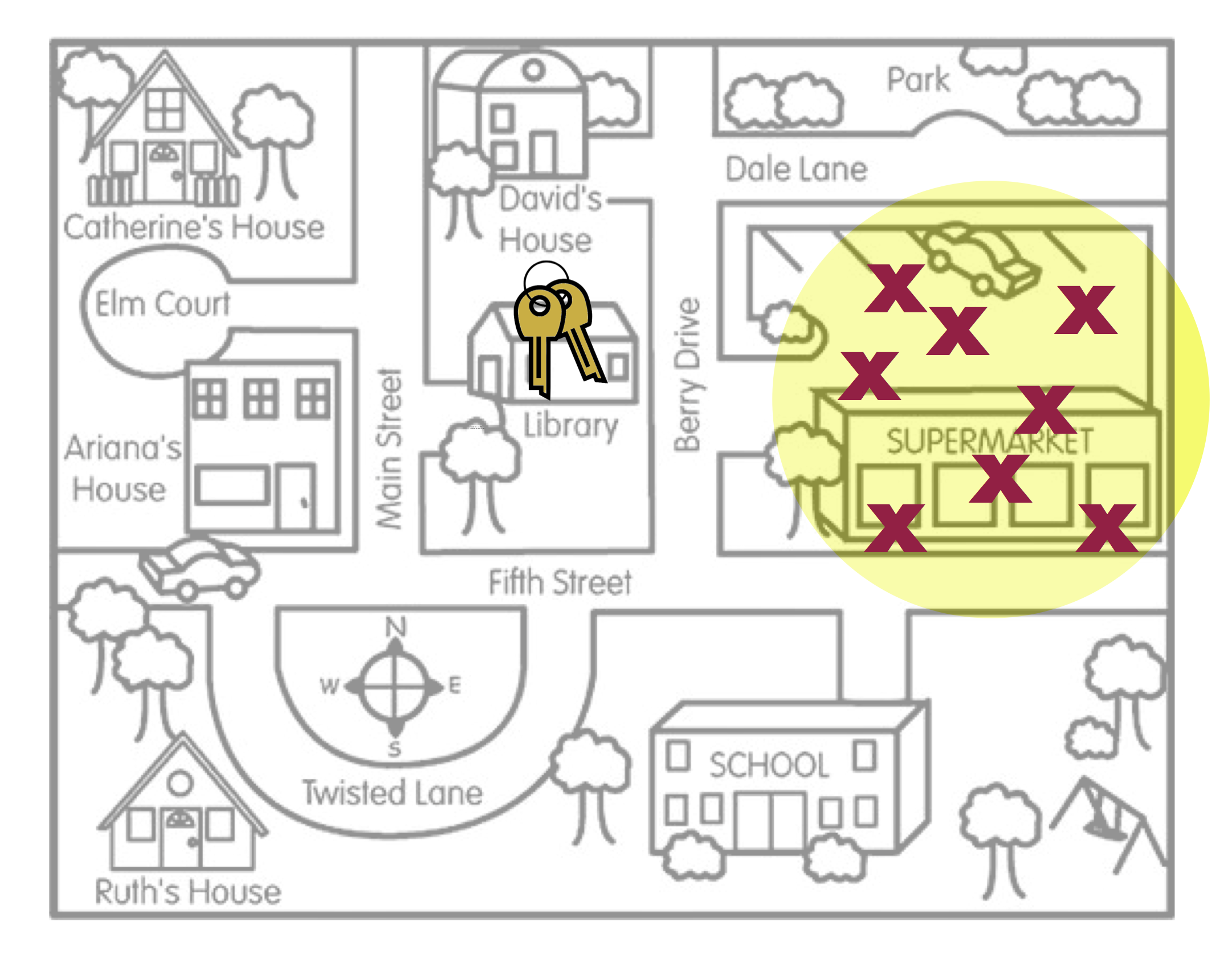
To help you think about bias, imagine a person, Arthur Dent, has lost his keys. The actual location of the keys, the Library, is akin to the population parameter. Arthur believes he lost his keys at the Supermarket and searches several places around the Supermarket. The locations where Arthur searches are like sample statistics.


This figure is a metaphor for statistical bias.
Figure 1: This figure is a metaphor for statistical bias.


Figure 1 is a metaphor for the concept of statistical bias. Arthur’s search locations (sample statistics) are systematically in the wrong place. On average, where Arthur searched (the middle of the yellow circle) is not the actual location of the keys. Compare this with the search locations in Figure 2.


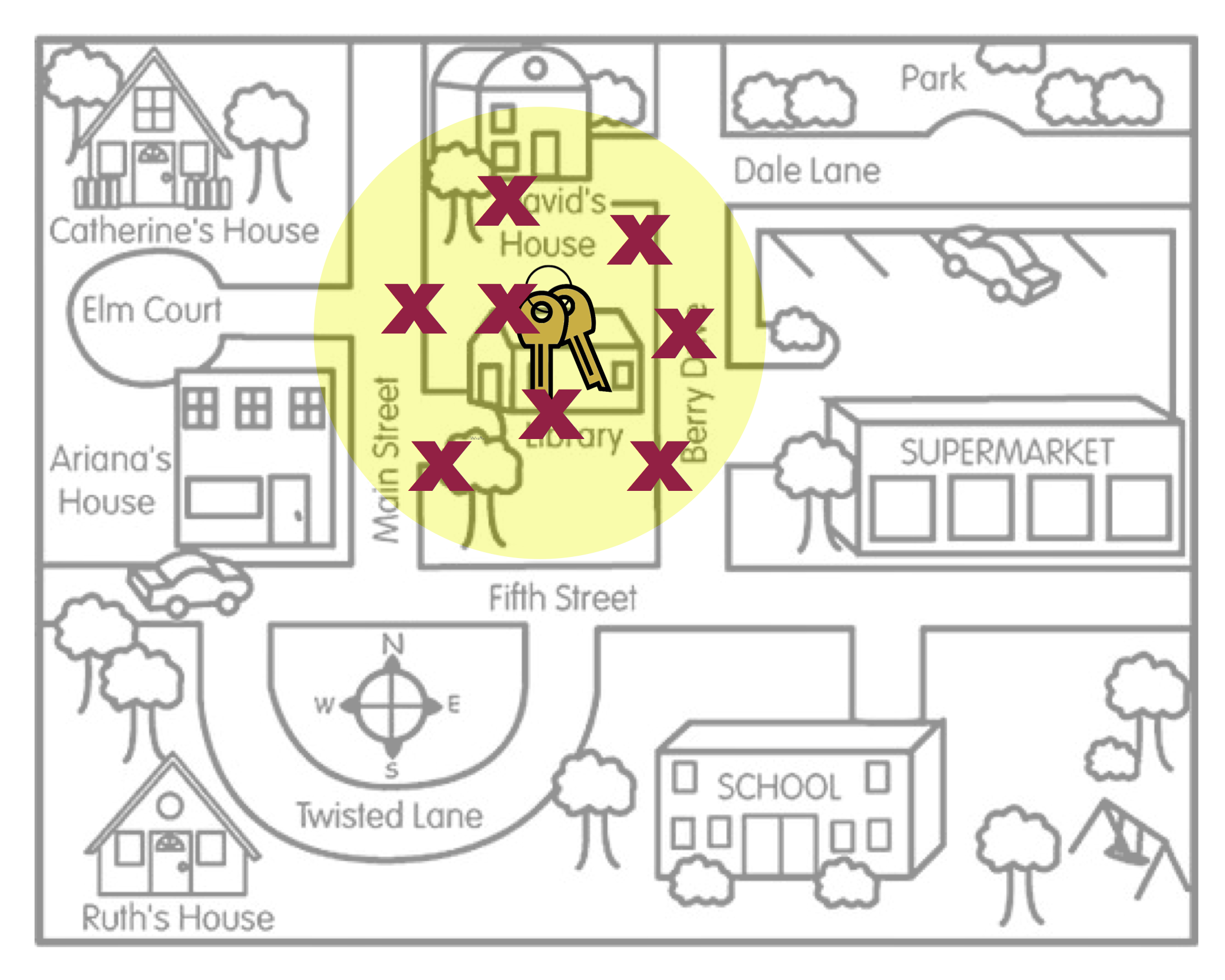
This figure is a metaphor for unbiasedness.
Figure 2: This figure is a metaphor for unbiasedness.


Figure 2 is a metaphor for unbiasedness. On average, where Arthur searched is the location of the keys. There are a couple of other concepts that this metaphor can help us think about.

  1. Even in Figure 2, none of the actual search locations were right at the keys. Some of the locations were too far to the left of the keys, and others were too far to the right of the keys. However, ON AVERAGE, the search locations “found” the keys. The way we define unbiased is that the AVERAGE of the statistics is at the population parameter.

  2. Average has nothing to do with the size of the yellow circle. (The size of the circle is related to the amount of sampling variation, a concept we will deal with in Unit 4.) The two figures in Figure 3 (below) also illustrate unbiasedness (left) and bias (right), despite the size of the yellow circle.

  3. The last concept about bias to point out is that bias (or unbiasedness) is a property of the sampling method. The reason the search locations were not in the right place is because the method Arthur used to pick the search locations was biased. He thought he lost his keys in the Supermarket, so that is where he looked.

Bias and sampling variation are two different ideas.
(a) Unbiased sample with the a lot of sampling variation.
Bias and sampling variation are two different ideas.
(b) Biased sample with the very little sampling variation.
Figure 3: Bias and sampling variation are two different ideas.


Unbiased Sampling Method

The key to whether study results generalize to the larger population is whether the sample cases were selected from that population using an unbiased sampling method. One unbiased sampling method is random sampling. Random sampling uses chance to select the sampling units (participants) from the larger population. When random sampling has been employed in a study, the unbiasedness of the sampling method is strong evidence for generalization; we have a much higher belief in generalizations to the larger population.

There are many random sampling methods employed by researchers. For example:

The most elementary of these methods is simple random sampling. To draw a simple random sample we need a list of EVERY member of the population. This list is called the sampling frame. (Obtaining a sampling frame can be very difficult. Try obtaining a list of everyone who lives in the United States!) Then we employ randomness to draw out sampling units, with the caveat that each unit in the sampling frame has an equal chance of being drawn.

This is akin to drawing names out of a hat. Everyone’s name is written down (the sampling frame) and added to the hat. Then a chance mechanism is employed to draw out a name. Ideally, there would be no sytematic bias in the selection of names from the hat (e.g., all the pieces of paper would be the same size; the person drawing would be equally likely to draw a name from the top of the hat as the bottom of the hat).

KEY QUESTION FOR GENERALIZATION

One key question to ask when you are considering whether generalizations are appropriate is: How were the sample cases selected? If the answer is they were selected using an unbiased sampling method like simple random sampling, then your sample findings do generalize to the population. If the answer is that they were not selected using an unbiased sampling method, then the sample findings probably do NOT generalize to the population.